En física clásica, dos conceptos fundamentales que se utilizan a menudo para describir magnitudes físicas son los vectores y los escalares. Es importante entender estos dos conceptos porque tienen propiedades distintas que son útiles para describir el mundo físico.
Un escalar es una magnitud física que tiene magnitud pero no dirección. Ejemplos de escalares son la temperatura, la masa y el tiempo. Las magnitudes escalares se pueden sumar y restar igual que los números. También se pueden multiplicar o dividir por un número.
En cambio, un vector es una magnitud física que tiene magnitud y dirección. Ejemplos de vectores son la velocidad, la aceleración y la fuerza. Los vectores se representan gráficamente mediante flechas. La longitud de la flecha representa la magnitud del vector, y la punta de la flecha representa la dirección del vector. Los vectores no se pueden sumar ni restar como los escalares. En su lugar, las operaciones de los vectores satisfacen la regla del paralelogramo o la regla del triángulo.
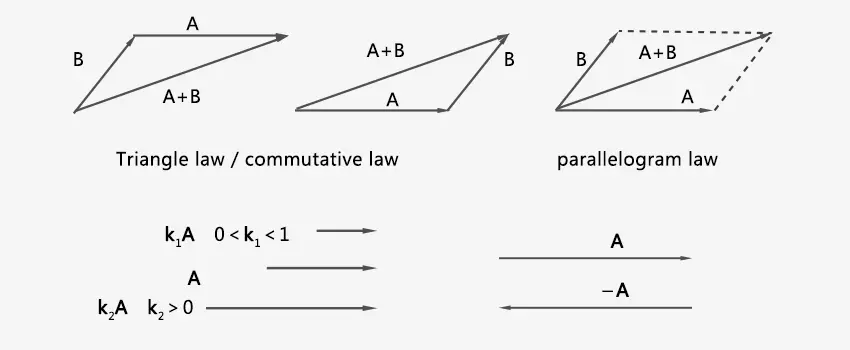
La suma de vectores satisface la ley conmutativa: A+B=B+A
La suma de vectores satisface las leyes asociativas: (A+B)+C=A+(B+C)
Un vector puede multiplicarse por un escalar: k x A = kA. Si k < 0, la dirección de kA es opuesta a la de A. Si k > 0, la dirección de kA es la misma que la de A. La longitud de kA está relacionada con k. Si |k| > 1, A se alarga un factor k. Si |k| < 1, A se acorta un factor k. Si |k| = 1, su longitud no varía. -A se obtiene girando el vector original 180°.
Vectores en coordenadas rectangulares o cartesianas
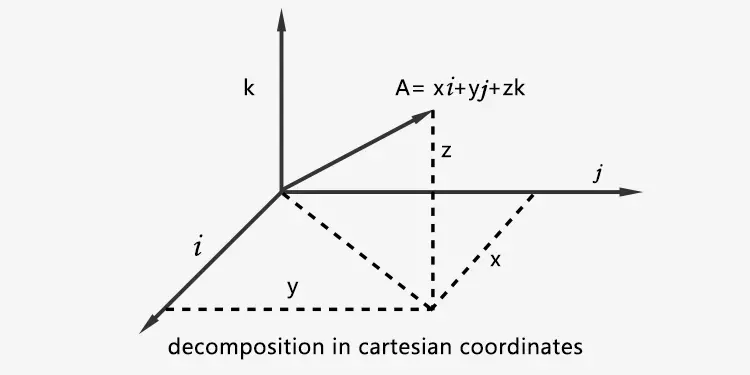
A está en el plano:A = xi + yj = (x,y)
A está en el espacio:A = xi + yj + zk = (x,y,z)
A + B = (x,y,z) + (t,v,w) = (x+t,y+v,z+w)
kA = k(x,y,z) = (kx,ky,kz)
La longitud de A está representada por |A| = √(x²+y²+z²), la dirección de A está representada por un vector unitario e = A/|A|.
Otra diferencia importante entre vectores y escalares es que los vectores pueden resolverse en componentes. Es la inversa de la suma de vectores y la descomposición es arbitraria (la suma de ellas debe volver a ser el vector original). Puedes elegir el método más beneficioso según tus necesidades. Normalmente los vectores se descomponen a lo largo de los ejes de coordenadas si se dispone de una coordenada cartesiana. Por ejemplo, un vector bidimensional, o un vector en un plano, puede resolverse en sus componentes x e y, que son escalares que describen la velocidad en las direcciones horizontal y vertical, respectivamente.
Existen dos tipos de multiplicación vectorial: el producto punto y el producto cruz.
El producto punto es un escalar.
A·B = |A||B|cosθ = xt + yv +zw, θ es el ángulo entre los vectores A y B.
si B=A, θ=0°, cosθ=1 y A·A = |A|².
si A es perpendicular a B, θ=90°, cosθ=0 y A·B = 0.
Su producto cruzado es vectorial.
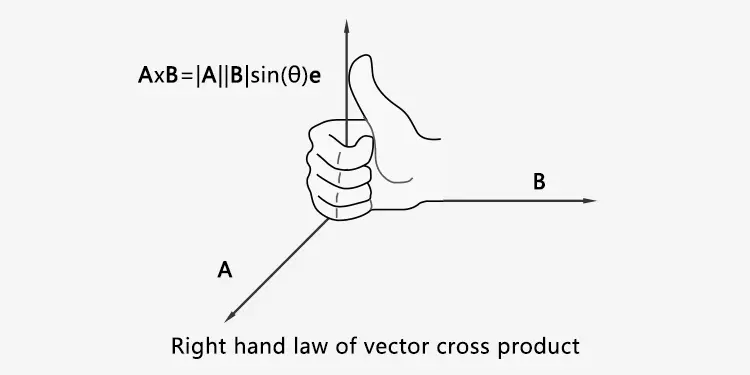
AxB = |A||B|sinθ e = (yw-zv,zt-xw,xv-yt), θ es el ángulo entre los vectores A y B. El vector e es perpendicular al plano en el que se encuentran A, B y e, A, B satisfacen la regla de la mano derecha.
si B es paralelo a A, θ=0°, sinθ=0 y AxB = 0.
si B=A o B=-A, θ=0°, sinθ=0 y AxA = -AxA = 0.
si A es perpendicular a B, θ=90°, sinθ=1 y AxB = |A||B|e. En esta condición la longitud de AxB es máxima.