Cuando la aceleración es constante y su dirección es paralela a la velocidad inicial, el objeto se mueve a lo largo de una línea recta con aceleración uniforme. Es un ejemplo especial de movimiento acelerado.
Movimiento lineal uniformemente acelerado: velocidad, aceleración y tiempo.
Puedes hacer la fórmula más concisa reemplazando Δt por t.
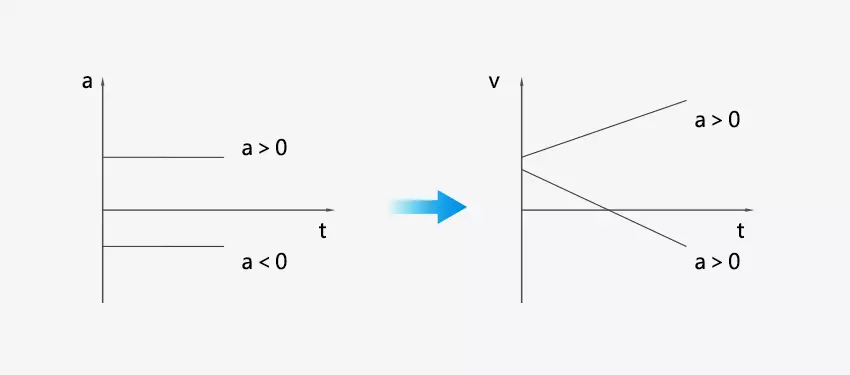
Dado que la aceleración es constante, el gráfico de tiempo de velocidad es una línea inclinada o una función lineal. Una línea recta inclinada hacia abajo indica una dirección de aceleración negativa y es opuesta a la dirección positiva que se definió inicialmente. Una línea recta inclinada hacia arriba indica una dirección de aceleración positiva.
Cuando la aceleración es en la misma dirección que la velocidad inicial, el objeto se acelera. Cuando la aceleración es en dirección opuesta a la velocidad inicial, el objeto se desacelera y luego se acelera en dirección opuesta.
Movimiento rectilíneo uniformemente acelerado: desplazamiento, velocidad inicial, aceleración y tiempo.
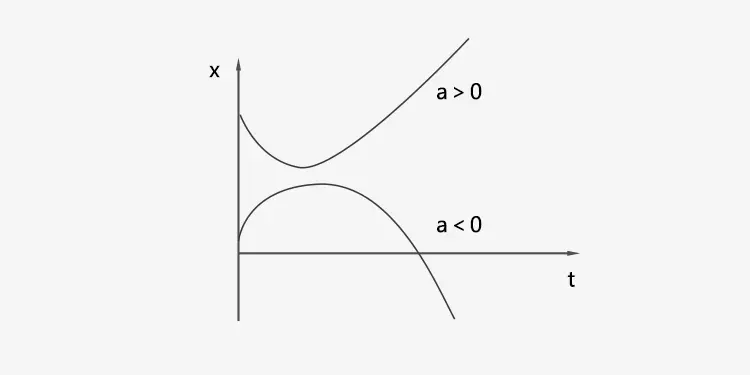
Dado que la aceleración es constante, la gráfica de desplazamiento-tiempo es una curva cuadrática. Su línea tangente representa la velocidad.
La curva cóncava ⇔ a < 0, la dirección de aceleración es opuesta al eje x. La curva convexa ⇔ a > 0, la dirección de aceleración es la misma que el eje x.
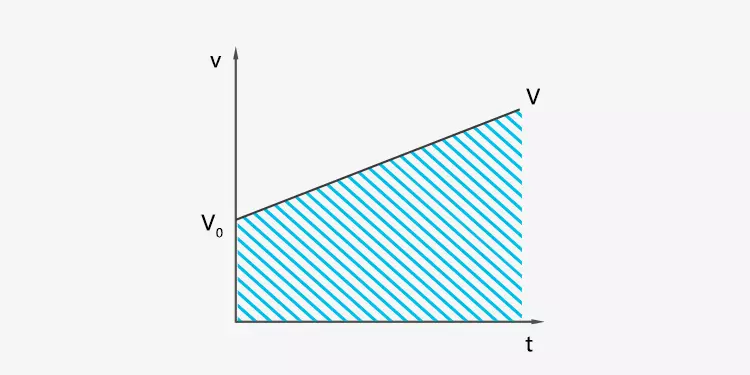
El desplazamiento es el área encerrada por la curva y el eje t en el gráfico v-t. Esto es equivalente a resolver el área de un trapezoide.
Sustituye v en la ecuación ① por esto.
Ambos lados de la fórmula ① dividido por t puede obtener la velocidad media en el intervalo de tiempo de t.
La velocidad media también es igual a la velocidad en el momento intermedio.
Movimiento rectilíneo uniformemente acelerado: desplazamiento, velocidad y aceleración
,
Eliminando t se obtiene una fórmula para el desplazamiento y la velocidad.
v² - v₀² = 2a(x - x₀)
Velocidad de medio desplazamiento
Un objeto se desplaza de A a B con aceleración uniforme, hallar la velocidad en el punto medio de AB. La velocidad del objeto en A es v₀, la velocidad en B es v₁, la velocidad en el punto medio de AB es v , el desplazamiento x - x₀ de A a B, y el intervalo de tiempo entre A y B es t .
La aceleración de la mayoría de los movimientos no es constante, entonces ¿cuál es la importancia de estudiar el movimiento lineal con aceleración constante?
Es el movimiento no uniforme más simple, por lo que sus detalles son los más fáciles de explorar claramente.
Además, existen algunos movimientos comunes que pertenecen al movimiento uniformemente acelerado, como lanzar objetos hacia arriba o hacia abajo y la caída libre.
En muchos casos, no necesitamos estudiar cada detalle del movimiento con precisión como lo hacen los científicos. Solo queremos obtener conclusiones rápidas y semi-cuantitativas, por lo que es significativo aproximar el movimiento real como un movimiento uniformemente acelerado. Por ejemplo, el arranque de un automóvil y una bala que entra en un bloque de madera se pueden considerar como movimientos con aceleración constante.
¿Cómo se puede resolver el problema del movimiento lineal uniformemente acelerado?
Si la velocidad, el desplazamiento y la aceleración en estas fórmulas son positivos o negativos dependerá del sistema de coordenadas que establezcas. Si necesitas ingresar valores en las ecuaciones, el primer paso debe ser establecer un sistema de coordenadas para determinar el signo de los valores. Generalmente, este tipo de problemas son relativamente simples y se pueden calcular directamente ingresando los números en la fórmula. Los problemas más difíciles requieren escribir la función de desplazamiento del objeto en función del tiempo.
¿Cuándo se encontrarán A y B?
El objeto A con velocidad constante está persiguiendo al objeto B, que se mueve con aceleración constante. La distancia entre ellos es s. La velocidad del objeto A es vₐ, mientras que la velocidad inicial del objeto B es v₀ y la aceleración de B está en la misma dirección que la velocidad inicial.
Dado que todas las velocidades y aceleraciones están en la misma dirección, podemos asumir que la dirección positiva del sistema de coordenadas es la misma que la dirección de la velocidad.
Xₐ = vₐt
Xᵦ = s + v₀t + at²/2
F(t) = Xᵦ - Xₐ= s+ (v₀- vₐ)t + at²/2
Cuando F(t) = 0, A se encuentra con B. Esto es equivalente a resolver una ecuación cuadrática. La ecuación tiene una solución cuando Δ = (v₀ - vₐ)² - 2as ≥ 0.


