Average acceleration & Instantaneous Acceleration

Uniform motion is one of the simplest motions. Few objects are moving at constant velocity; most objects are moving at variable velocity. Some objects can reach high speed motion in a much shorter time. For example, a bullet train and a race car can both reach a speed of 300km/h, but the race car takes only a few seconds and the train takes several minutes. Obviously the concepts of displacement and velocity are not enough to describe the object's motion well. The new physical concept we want to define is acceleration: the change of velocity divided by the time interval.

$a=\frac{\mathrm{\Delta v}}{\mathrm{\Delta t}}=\frac{\mathrm{v₂\; -\; v₁}}{\mathrm{t₂\; -\; t₁}}$

Δv represents the change of velocity; Δt represents the time interval. The international unit of acceleration is meters per second squared(m/s²).

Acceleration measures how fast an object changes its velocity. It is a vector with magnitude and direction. Its direction is the same as the direction of velocity change over a given time interval.

Average acceleration

Similar to velocity, acceleration varies continuously in most cases. If Δt is finite, then the acceleration calculated by the above formula is the average value over the Δt interval. It does not represent the acceleration at a moment.

Instantaneous acceleration

If we want to describe the motion of an object more precisely, we need to know the acceleration at each moment. If Δt is very small, the average acceleration will be close to the instantaneous acceleration. When Δt tends to zero, the average acceleration becomes the instantaneous acceleration.

Relationship between acceleration and velocity

1. The direction of acceleration is parallel to velocity.

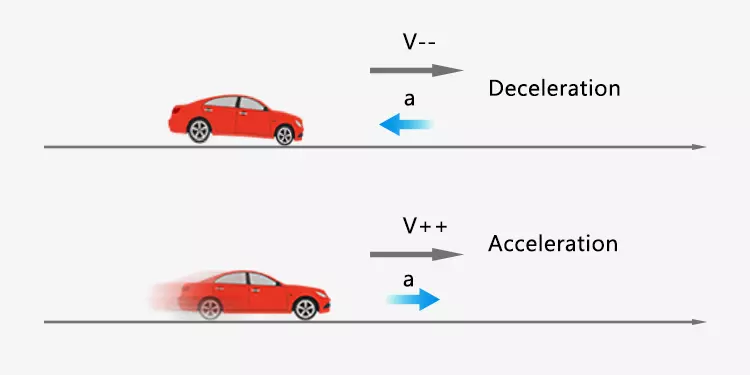
The object moves in a straight line. If the direction of velocity is the same as acceleration, then the object accelerates. If the direction of velocity is opposite to acceleration, then object decelerates. If the decelerating motion lasts for a long time, the velocity will become zero. Then the object accelerates with zero initial velocity. Now its velocity direction is the same as the acceleration direction, but opposite to the original velocity direction.

2. The direction of acceleration is perpendicular to the velocity.

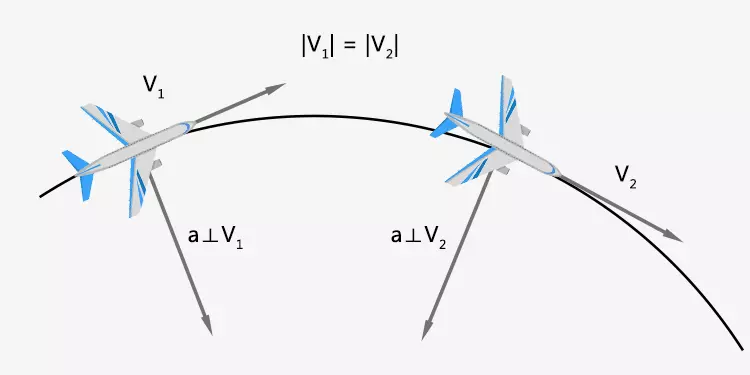
The magnitude of object's velocity remains the same, but the direction changes.

3. The direction of acceleration is not parallel to the velocity and is also not perpendicular.

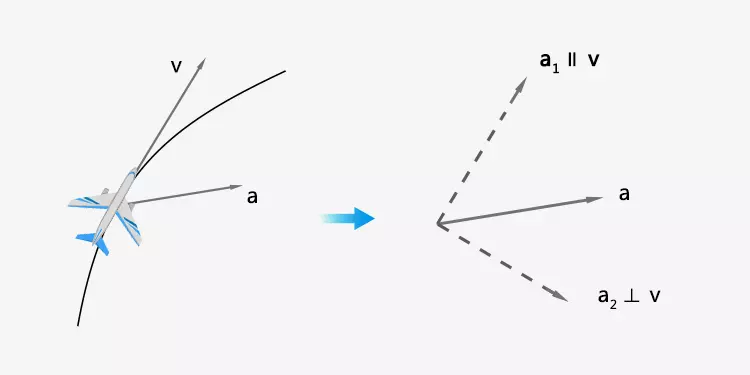
You can decompose the acceleration into two components, one parallel to the velocity and the other perpendicular to it. How these two accelerations affect the motion has been discussed above. In this case, both the magnitude and the direction of the velocity change.