Once we have established the coordinate system and represent object positions as the vectors in coordinate system, we can study the displacement of object. It is a fundamental concept in classical physics that describes the change in position. It is defined as a difference between two vectors: the starting point vector subtracts from the ending point vector, taking into account both magnitude and direction.
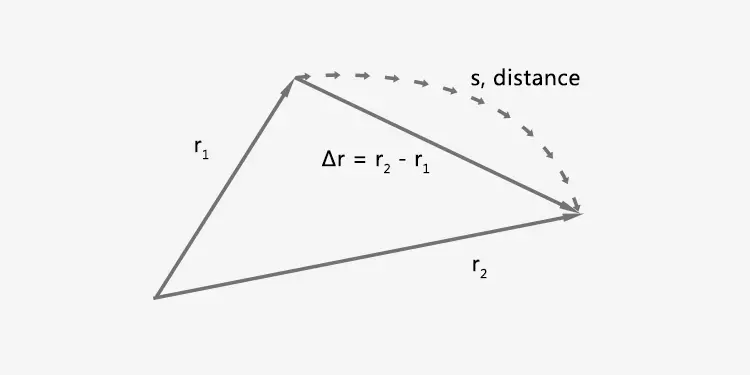
Displacement can be calculated using the formula:
Δr = r₂ - r₁
Where Δr represents the displacement vector, r₁ represents the starting position, and r₂ represents the ending position. The SI unit for displacement is meters (m).
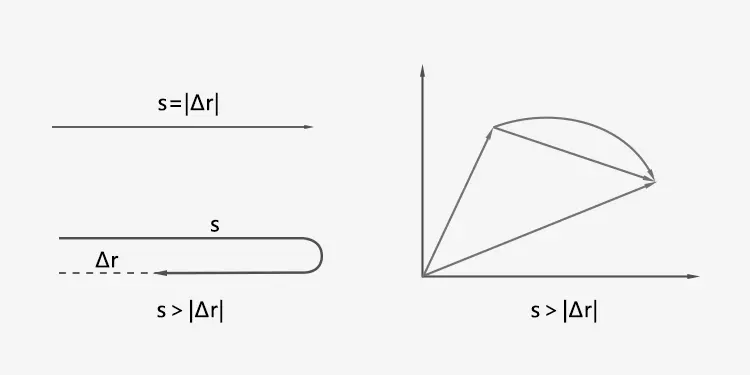
Displacement and distance are often confused with each other.
Distance is a positive scalar quantity that measures the length of the path taken by an object. For example, if an object moves from point A to point B and then back to point A, the total distance covered by the object is the sum of the distance from A to B and the distance from B to A.
On the other hand, displacement is a vector that measures the position change. It takes into account both magnitude and direction. It is determined by the start and end positions, independent of the path. For example, if an object moves from point A to point B and then back to point A, the displacement is zero because its final position is the same as its initial position.
Calculate the displacement in one dimension coordinate system or the number line
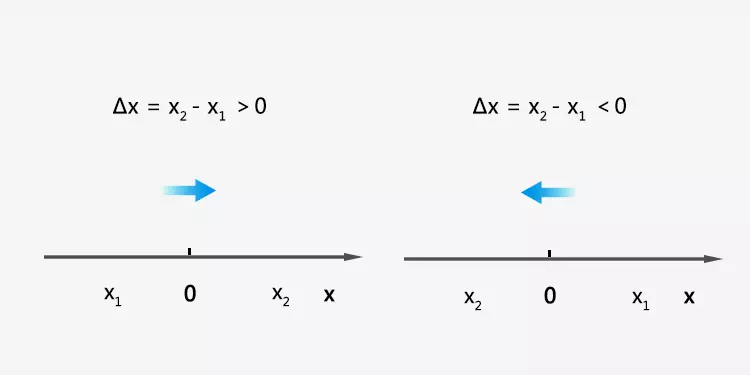
The coordinates of the starting point are x₁ and the coordinates of the ending point are x₂. Displacement is Δx = x₂ - x₁ . If Δx > 0, the direction of displacement is the same as the direction of the coordinate axis. If Δx < 0, the direction of displacement is opposite to the direction of the coordinate axis. If Δx = 0, the starting point coincides with the end point.
Calculate the displacement in three dimensional coordinate system
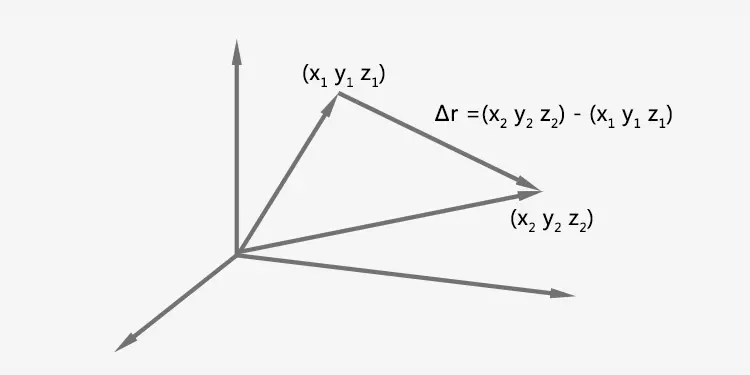
The displacement is decomposed along each axis to calculate its components. In this way we have simplified the three-dimensional problem to a one-dimensional one.
Δr = r₂ - r₁ = (x₂ - x₁)i + (y₂ - y₁)j + (z₂ - z₁)k