We need to determine which objects are moving faster in many cases. A common way to compare them is to see which one moves longer distances in the same time. Another common method is to compare which of them takes less time over a given distance. These are relatively crude methods, especially when the two objects cannot compete like athletes in a race. For example, to determine whether a flea jumps faster than an airplane.
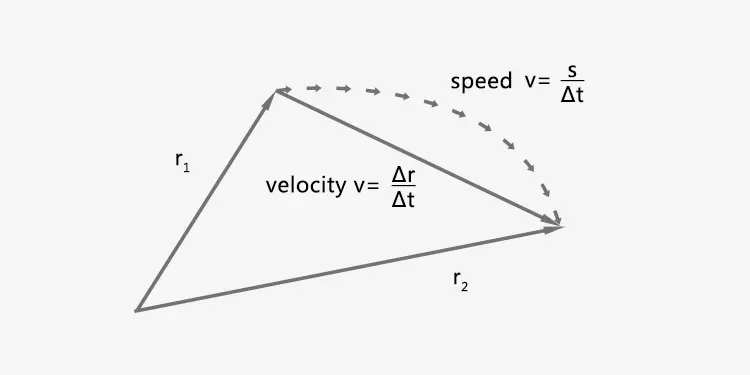
We need new concepts to research motion. We already have the concept of displacement, a more natural way to define velocity is to divide displacement by the time interval.
Δr represents the change of position or displacement; Δt represents the time interval. The international unit of velocity is meter per second (m/s), and other common unit is kilometer per hour (km/h).
Velocity is a measure of how fast an object moves in a given time. It is a vector because it has magnitude and direction. Its direction is same as direction of the position change during a specific time interval, or the direction of displacement.
Average velocity
If the time interval Δt is a finite quantity, which you can also interpret Δt is not very small, then the v calculated by the above formula is the average velocity during the time interval Δt. In general, the average velocity can not represent the velocity at a specific moment, because the magnitude and direction of the object velocity usually changes in the time interval.
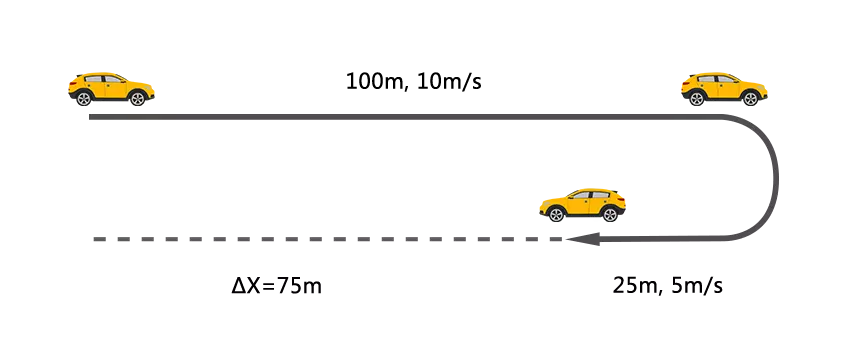
For example, if a car travels 100 meters east in 10 seconds, then 25 meters west in 5 seconds, its total displacement is 75 meters east. The total time it takes to travel this distance is 15 seconds.
The average velocity of car: v = 75 m / 15 s = 5 m/s, toward the east.
The car velocity is changing as it travels: from 10 m/s toward the east to 5 m/s toward the west.
Average speed
If one wants to know the length of the path that an object passes through in certain time interval, rather than the change of position. The average speed is introduced to describe it.
The s represents distance travelled; the Δt represents time interval. Like the average velocity, the international unit of average speed is the meter per second (m/s), while the other commonly used unit is the kilometer per hour (km/h).
Since distance represents the total length of the path traveled and is not related to direction, the average speed has no direction, only numerical magnitude.