Uniformly Accelerated Motion in a Striaght Line

When the acceleration is constant and its direction is parallel to the initial velocity, the object moves along a straight line with uniform acceleration. It is a special example of accelerated motion.

Uniformly accelerated linear motion: velocity, acceleration and time

$a=\frac{\mathrm{\Delta v}}{\mathrm{\Delta t}}=\frac{\mathrm{v\; -\; v₀}}{\mathrm{t\; -\; t₀}}\Rightarrow$$\mathrm{<br>}$

$\mathrm{\Delta v}=\mathrm{a\Delta t}\Rightarrow$$\mathrm{<br>}$

$v=\mathrm{v₀\; +\; a\Delta t}\Rightarrow$

$$$v=\mathrm{v₀\; +\; at}$

You can make the formula more concise by replacing Δt with t.

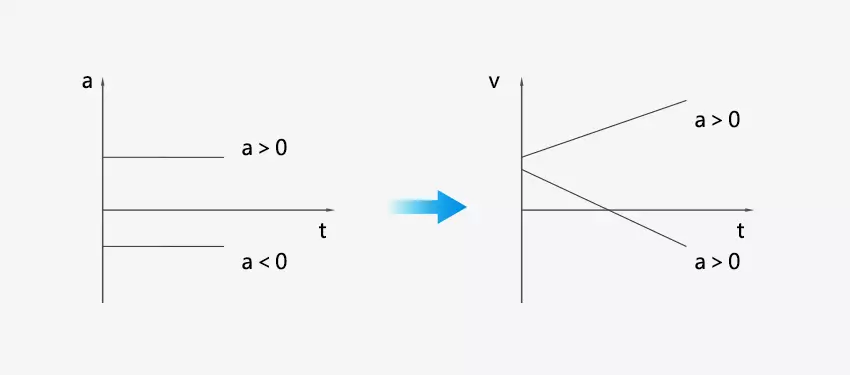
Since the acceleration is constant, the velocity-time graph is a sloping line, or it is a linear function. A straight line sloping downward indicates a negative direction of acceleration and it is opposite to the positive direction you prescribed. A straight line sloping upward indicates a positive direction of acceleration.

When the acceleration is in the same direction as the initial velocity, the object accelerates. When the acceleration is in the opposite direction of the initial velocity, the object decelerates and then accelerates in the opposite direction.

Uniformly accelerated rectilinear motion: displacement, initial velocity, acceleration and time

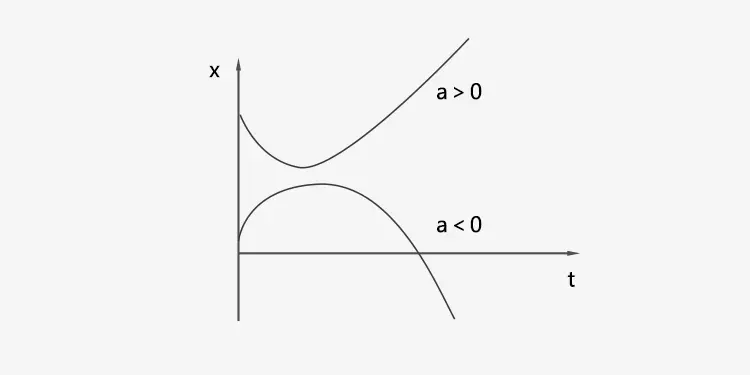
Since the acceleration is constant, the displacement-time graph is a quadratic curve. Its tangent line represents the velocity.

The concave curve ⇔ a ＜ 0, the acceleration direction is opposite to the x-axis. The convex curve ⇔ a > 0, the acceleration direction is the same as the x-axis.

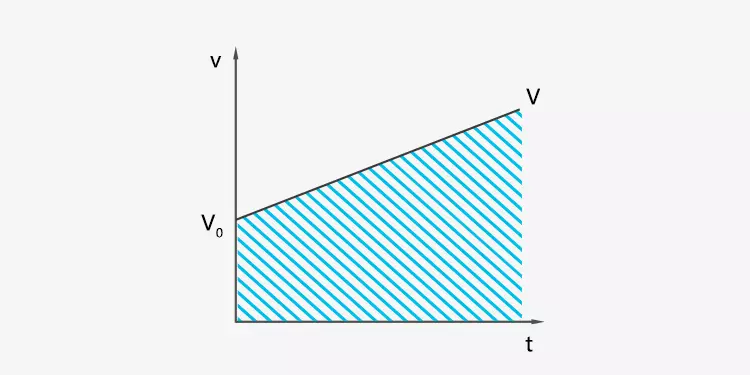
The displacement is the area enclosed by the curve and t axis in the v-t graph. This is equivalent to solving for the area of a trapezoid.

$\mathrm{x\; -\; x₀}=\frac{\mathrm{(v\; +\; v₀)t}}{2}\mathrm{·····························①}$

$v=\mathrm{v₀\; +\; at}$Replace v in equation ① with this.

$\mathrm{x\; -\; x₀}=\mathrm{v₀t\; +}\frac{\mathrm{at²}}{2}\mathrm{·····························②}$

Both sides of formula ① divided by t can get average velocity in the time interval of t.

$\mathrm{Average\; velocity}=\frac{\mathrm{x\; -\; x₀}}{t}=\frac{\mathrm{v\; +\; v₀}}{2}$

The average velocity is also equal to the velocity at the intermediate moment.

$\frac{\mathrm{v\; +\; v₀}}{2}=\frac{\mathrm{v₀\; +\; v₀\; +\; at}}{2}=\mathrm{v₀\; +}\frac{\mathrm{at}}{2}=V_{\mathrm{t/2}}^{}$

Uniformly accelerated linear motion: displacement, velocity and acceleration

$\mathrm{x\; -\; x₀}=\frac{\mathrm{(v\; +\; v₀)t}}{2}$,$t=\frac{\mathrm{(v\; -\; v₀)}}{a}$

Eliminating t results in a formula for displacement and velocity.

v² - v₀² = 2a（x - x₀）

Velocity of one half displacement

An object moves from A to B with uniform acceleration, find the velocity at the midpoint of AB. The velocity of the object at A is v₀, the velocity at B is v₁, the velocity at the midpoint of AB is v , the displacement x - x₀ from A to B, and the time interval between A and B is t .

$\mathrm{v²\; -\; v₀²\; =\; 2a（x\; -\; x₀）\; ÷\; 2\; =\; a(x\; -\; x₀)=\; a\; t}\stackrel{—}{v}$

$\mathrm{at\; =\; v₁\; -\; v₀,}\stackrel{—}{v}=\frac{\mathrm{v₁\; +\; v₀}}{2}\mathrm{Plug\; these\; two\; formulas\; into\; the\; first\; one.}$

$\mathrm{v²\; -\; v₀²\; =\; (v₁\; +\; v₀)(v₁\; -\; v₀)\; ÷\; 2}\Rightarrow \mathrm{v²\; =\; (v₀²\; +\; v₁²)/2}$